Briefwechsel Georg Moritz Lowitz
| Kurzinformation zum Brief | |
| Autor | Lowitz, Georg Moritz (1722-1774) |
| Empfänger | Euler, Leonhard (1707-1783) |
| Ort | Nürnberg |
| Datum | 20. Dezember 1749 |
| Signatur | Archiv der Akademie der Wissenschaften, St. Petersburg: F. 136. Op. 2, Nr. 2, Bl. 79-80r |
| Zusammenfassung | Juškevič, Adolf Pawlowitsch; Winter, Eduard: Die Berliner und die Petersburger Akademie der Wissenschaften im Briefwechsel Leonhard Eulers. Band III, Teil 3. Berlin: Akademie-Verlag 1976, S. 211-214 |
| Fußnoten | Hans Gaab, Fürth |
Obwohl Lowitz weiß, daß Eulers Zeit außerordentlich kostbar ist, muß er ihm in "beiliegendem Avertissement" in den §§ 46-53 " eine große Bitte" vorlegen.[1] Er dankt vor allem für die ausführliche Antwort Eulers auf sein Schreiben vom vergangenen Jahr[2] und für "Dero darinnen gegebenen Lehren". Vor allem dankt er für die "Auflösung" der Formeln.
Lowitz hatte in seiner Frage zu den Rotationsflächen den Begriff "vollkommen ähnlich" gebraucht, was nicht "vollkommen gleich" bedeutet. Er sieht ein, daß das Wort "vollkommen" dabei überflüssig ist. Lowitz legt seine Gedanken dazu dar und bittet um Eulers Urteil, ob diese wert sind, in den "Ephemeriden unserer Gesellschaft" veröffentlicht zu werden.
Weiter schreibt Lowitz: "Im Anfang habe ich mir eine geradlinichte Figur auf einer Fläche vorgestellt, die nach Gefallen gegen eine andere Fläche geneigt ist, und die Natur der Proportion untersucht, wenn sie soll der Figur selbsten gleich und ähnlich sein. Es eie demnach in beistehender Figur ABC ein Dreieck, das mit seines Spitze B auf der Projektionsfläche DQM aufstehet, über derselben aber unter einem Winkel CEM geneiget ist.
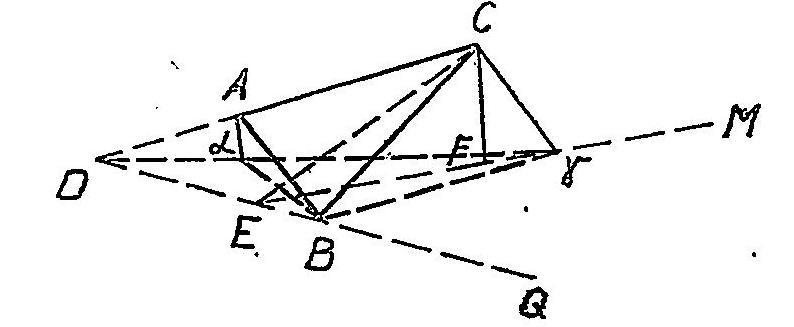
Es sei ferner DQ der gemeinschaftliche Durchschnitt der Fläche dieses Dreiecks mit der Projektionsfläche, und die verlängerte Seite AC fußt in D. Die Linie CE ist von der Spitze C zur Linie DQ perpendikular gezogen. Lässet man auch aus C zur Projektionsfläche die Perpend[ikular]-Linie CF herunterfallen und ziehet von E durch F die Linie EM, so wird die Spitze C des Dreiecks auf dieser Linie in γ und die Spitze A auf der Linie Dγ in α fallen. Es ist also das Dreieck αBγ dem Dreieck ABC gleich, wenn nämlich das Dreieck ABC um den Durchschnitt DQ niedergelegt wird, welches ich bald zu erinnern vergessen hätte. Es war also nur nötig, die Lage der Linien Cγ und Aα zu bestimmen, um ein Dreieck αBγ dadurch hervorzubringen, das dem ABC gleich und ähnlich seie. Wenn man in dem Fall, da die Figur eine glatte Fläche ist, nun die Lage einer einzigen solchen Linie hat, so werden die anderen alle dieser parallele sein.
Ich habe also gefunden, daß diese Linie erstlich in derjenigen Fläche liegt, in welcher die Perpendikularlinie CF und die zu C auf die Fläche des Dreiecks gezogene Normale sich befindet, und daß sie zum andern denjenigen Winkel, welchen diese beiden erstgemeldten Linien miteinander machen, in zwei gleiche Teile teilet. Lässet man nun von jedem Punkte C auf die Projektionsfläche die Pepen[ikular]-Linie CF herunterfallen und zie[he] auch zu dem Punkt C auf die Fläche der vorzustellenden Figur die Normal CN und vereinigt F und N, so wird, wann F&gamm; = (CF * FN) / (CR + CN), ds Punkt γ die Projektion des Punktes C sein. Es ist also klar, daß, wann die Normallinien CN alle unter sich parallel sind, die Projektion der Figur selbsten gleich und ähnlich wird, außer diesem aber oder bei krummen Flächen wird nur die Ähnlickeit ohne die Gleichheit zu erhalten sein.
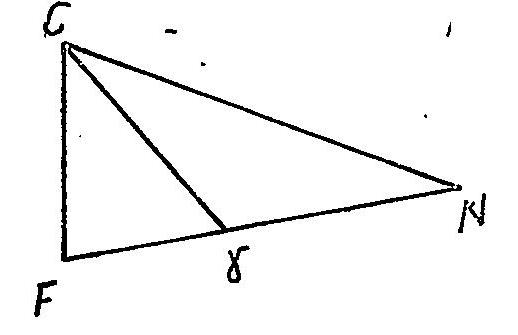
Euer Hochedelgeboren wissen ohnehin mehr als zu wohl, daß diese Betrachtung auf die Oberflächen aller Körper anzuwenden ist. Ich will demnach nur soviel sagen, daß auf diesem Weg durch Hilfes des 68.§ des II. Tomi Ihrer ohnvergleichlichen Mechanik gefunden, daß wann für eine jede Oberfläche eines Körpers AP = x, PM=y, MN = z und die Differentialgleichung dieser Oberfläche δZ = A δx + B δy, und endlich γ das erklärte projezierte Punkt Punkt von N ist, so wird sein, wenn πγ mit PM parallel und zu AP perpendik[ular] gezogen wird
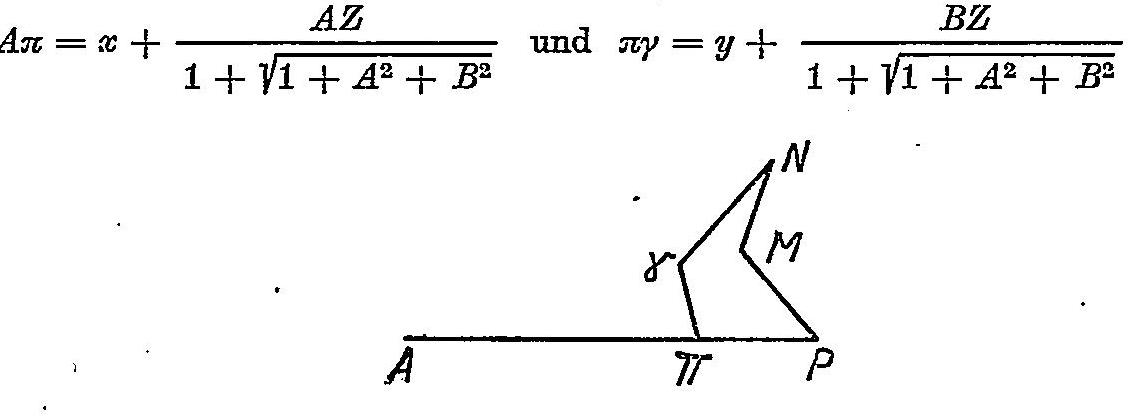
Über diese habe solche ebenfalls auf solche Körper insbesondere gerichtet, die durch die Umdrehung einer krummen Linie um eine Achse entstehen. Es sei zu diesem Ende πC die Achse eines solchen Körpers, die mit der Projektionsfläche HPM einen Winkel ΠCH = π macht. Ferner sei CV = v und VR = VN = t, durch welche Größe die Koordinaten des Meridians ΠRO angedeutet werden. wenn nun wiederum CP = x, PM = y, MN = z, so wird sein x2 + y2 + z2 - t2 - v2 = a und -v = z sinπ - x cosπ im Fall der gegenwärtigen Figur.
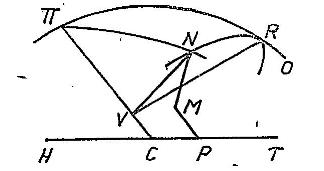
Ist nun eine Gleichung in t und v vergeben, welche die Natur des Meridians erklärt, so wird man nach der Ersetzung in die beiden gefundenen Gleichungen eine andere Gleichung in lauter x, y und z erhalten, die man folglich differenzieren und mit der allgemeinen Gleichung dz = A dx + B dy vergleichen kann, um die Größ A und B zu bekommen. Nimmt man endlich auch den Winkel RVN mit in die Rechnung und nennet solche = α, so ist x = t sin π cos α - v cos π und Y = t sin α und z = t cos π cos α + v sin π.
Ich muß der Kürze wegen alle Folgerungen übergehn und nur noch das Resultat der Anwendung auf die Sphäreis darstellen. Wenn also der Meridian eine Ellipse ist, deren halbe große Achse = 1 und der Unterschied der beiden Achesn = δ, und man nimmt 2&delta -δ2 = Θ, wo man das δ2 noch nicht negligieren mag, so ist die Gleichung zu dieser Ellipse v2 = (1 - Θ) - (1 - Θ)t2. Kennt man endlich auch den Winkel, welchen die Normal der Ellipse zu einem Punkt N mit der großen Achse machet = λ, welches zugleich die Breite des auf die Späreis übereinkommenden Orts mit andeutet, so wird sein:
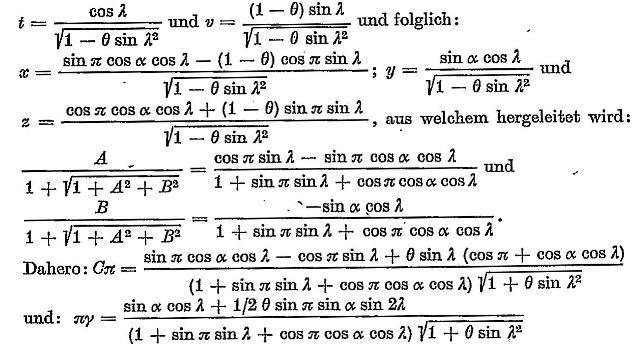
Diese Formeln sind vollkommen, so groß als auch δ immer sein mag". Lowitz hat diese Formeln nicht auf eine einfacher Form bringen können, woraus Euler sofort die Schwäche von Lowitz erkennen wird. Lowitz hofft aber, bei mehrfachen Durcharbeiten von Eulers Analysis infinitorum "schon noch so viele Kräfte" zu erlangen, wie sie für solche Aufgaben notwendig sind.
Lowitz war erfreut, im dritten Band der Historie de l'Academie soviele "herrliche Erfindungen" Eulers gefunden zu haben. Er hat sich sofort mit Spiritus gefüllte "Objektivgläser" machen lassen, wobei er zwischen verschiedenen Flüssigkeiten einen großen Unterschied in der Refraktion wahrgenommen hat, den er nicht erwartet hatte. Man muß die Gläser nach Eulers Vorschrift anfertigen lassen, "den es ist unmöglich, eben diejenigen flüssigen Mittel zu erhalten, die eben diejenige Refraktion geben als des Newtons sein." Lowitz hat eine "leichte und einfältige aber sehr gewisse Art" ausgesonnen, nach der er Objektive für ein 8-schuhiges Fernrohr herstellen läßt.
Lowitz hätte die "drei Paar kleinen Kugeln" schon längst übersandt, aber sie sind durch den Hund eines Gastes,
der der "zahmen Taube", die sich Lowitz hält, nachjagte, beschädigt worden. Ihm wurde der Schaden
zwar ersetzt, aber er hatte noch nicht die Zeit, sie wieder herzurichten, was aber in den nächsten Wochen erfolgen soll.
Als Beilage übersendet Lowitz ein nach Eulers "neuesten Tafeln im astronomische Kalender" angefertigtes
"Finsternißplättchen".[3]
Fußnoten
- ↑ In Bezug auf die Sternbilder, kann man sich die Erde von einer riesigen Glaskugel umgeben denken, auf der die Sternbilder aufgemalt sind. Wir befinden uns dabei im Innern der Kugel. Zeichnet man auf dem Himmelsglobus die Sternbilder so ein, wie man sie sieht (Himmelsansicht), sieht man sie auf dem Globus von Außen, nicht mehr von Innen. Deshalb wurden auf Himmelsgloben die Sternbilder in der Regel so eingezeichnet, als ob wir uns außerhalb der Glaskugel befinden würden (Globenansicht). Für diese Ansicht hat sich auch Lowitz entschieden. Denkt man sich aber nun die Sternbilder als tatsächliche Figuren, sieht man in Globenansicht nur ihrer Rückseite. Entsprechend wurden oft die K&oum;pfe der Figuren verdreht, dass man ihr Gesicht sehen konnte. Auf diese Weise entstanden aber teils unnatürliche Haltungen der menschlichen Figuren. Lowitz schlägt deshalb vor, sich die Figuren als auf der Glaskugel aufgemalte, durchsichtige Figuren vorzustellen. Sie sehen dann in beiden Ansichten gleich aus, lediglich links und rechts wechseln ihre Bedeutung. Nachdem Lowitz damit von der Tradition zahlreicher berühmter Astronomen abwich, wollte er sich der Meinung Eulers versichern, um nicht in den Ruf zu kommen besserwisserisch zu sein.
- ↑ Dieses Schreiben ist nicht überliefert.
- ↑ Diese Beilage ist nicht überliefert.
| voriger Brief an Euler | nächster Brief von Euler |


